Getting Started with R and SQL (Regardless of SQL Version) Using ODBC

Published November 29, 2017 / by shep2010

So here you are, you know SQL or you at least do something with it everyday and are wondering what all the hoopla is about R and data science. Lets break down the first barrier, R and data science actually have little to do with each other, R is a language, data science is an abstract field of work, sort of like saying I am a computer scientist, that will narrow it down but not by much. What is your industry, what languages do you use, what is your education, hacker, bachelors, masters, phd…? You can be a Data Scientist and never use R.

But we are going to use R, today, right now, get ready.

Continue reading →

Lets get started, again…

Published November 28, 2017 / by shep2010

The hardest thing about having a blog is without exception, having a blog! It will sit and wait for you forever to come back to it, I think about it every day and the hundred post that need to be completed. In my case, content is not the problem it’s the fact that some posts like this one will take a few minutes to one hour, and I have posts that have taken me two days to write, not because they were difficult, but because the technical accuracy of the post had to be perfect, or at least as perfect as I could come up with. I have already decided the first person I hire will be responsible for going back and verifying my posts… I feel sorry for them already.

Continue reading →

Fall 2017 SQL Intersections

Published September 12, 2017 / by shep2010

ITS HERE AGAIN!

The link to my sessions are here, which will lead you to other sessions as well.

This year there is an Analytics and Data Science track which includes the content i will be delivering related to SQL R, Data Science, and Visualization, but also Stacia Varga and David Pless delivering topics on Data Warehouse, SSIS, Reporting Services Mobile, and Power BI. Jam packed track, i am glad to see this.

I will be delivering my first Workshop this year, which means i am probably going to write 20 hours of content and scripts that i will attempt to stuff into 8 hours, all the better for you! The Workshop is Introduction to Statistical Learning and Graphics with SQL Server and R. That title is entirely too long, but here is what you get; The goal is to break down the intimidating barriers to R and find ways for you to use it everyday. Graphics are great troubleshooting tools, and i will have a few scripts and graphics for you to take into your everyday life. Additionally, using the ODBC package, you can connect to any version of SQL Server! This is independent of the Revolution R packages that ship with SQL, those can be used as well, but they are better saved for big data and data science stuff, but don’t fret we will be discussing that at a high level too.

Azure Burn

Published June 8, 2017 / by shep2010

I really like the title of this post, it is far more nefarious sounding that what this article truly is. What I mean is Azure burn rate, as in, how fast are you burning your Azure credits or real money.

My subscription, as do all new subscriptions, currently has a processor core cap of 20, which is normal and can be lifted in five minutes by opening a support ticket with MSFT from within Azure, instructions here. Incase you are wondering, MSFT will allow you to have 10,000 cores or more, and you will suddenly get very special attention from the entire company, so be reasonable in your request. I will be looking a AWS at some point, since I am no longer a MSFT employee my primary focus is the individual adopting new skills, not a specific platform. AWS has some interesting bid pricing for compute I am interested in. More later on that.

Continue reading →

Setting up a cloud Data Science test environment, on a budget

Published June 5, 2017 / by shep2010

Before I get into another long diatribe, know that the minimum you need to get started with R is R, and R Studio and know that they will run on just about anything. But if you want a bit more of an elaborate setup including SQL, read on.

Many years ago I took great pride in having a half dozen machines or more running all flavors of windows and SQL to play with and experiment on, it did not matter what it was, it would bend to my will. And in case you are wondering, NT would run very nicely on a Packard Bell.

Once I took over the CAT lab I was in hog heaven, I had a six figure budget and was required to spend it on cool fast toys and negotiate as much free stuff from vendors as I possible could. It was terrible, tough job to have. Jump forward to now, I own one Mac Book pro and one IPhone, and serves every need I have.
Continue reading →

Spring Intersections 2017

Published June 2, 2017 / by shep2010

Spring SQL Intersections 2017 is over, to those who attended I hope you enjoyed the sessions and found everything presented useful! I led the Data Science track this spring and plan on presenting many more sessions in the years to come. I have presented before, and I have presented at intersections before, but this was my first foray into original data science content, or to be more accurate, statistical learning content.

How do I Data Science?

Continue reading →

Histogram in a little more detail.

Published January 20, 2017 / by shep2010

We have covered histograms in several posts so far and if you have been around the block a few times you probably decided it was a bar chart. Well, thats kinda true, the x axis is represented of the data, age n the x axis for instance would simply be age sorted ascending from left to right and the y axis for a frequency histogram would be the number of occurrences of that age. The most important option being the number of bins, everything else is just scale.

Load up some data and lets start by looking at the barchart versions of the histogram. 


install.packages("mosaicData")
install.packages("mosaic")

library("mosaic")
library("mosaicData")


data("HELPmiss")
View("HELPmiss")

str(HELPmiss)

x <- HELPmiss[c("age","anysub","cesd","drugrisk","sex","g1b","homeless","racegrp","substance")]

#the par command will allow you to show more than one plot side by side
#par(mfrow=c(2,2)); or par(mfrow=c(3,3)); etc...

par(mfrow=c(1,2))

hist(x$age,col="blue",breaks=10)
hist(x$age,col="blue",breaks=50)

Using the code above you can see that the number of bins does change the graph too dramatically though some averaging clearly is taking place, but the x and y axis both make sense. We are basically looking at a bar chart, and based on shape we can derive some level of data distribution.

So, what happens when we add the line, the density curve, the PDF call it what you will? I have mentioned before it is a probability density function, but what does that really mean? And why do the numbers on the y axis charge so dramatically?

Well, first lets look at the code to create it. Same dataset as above, but lets add the "prob=TRUE" option. 



par(mfrow=c(1,2))
hist(x$age,prob=TRUE,col="blue",breaks=10)
hist(x$age,prob=TRUE,col="blue",breaks=50)

Notice the y axis scale is no longer frequency, but density. Okay, whats that? Density is a probability of that number occurring relative to all other numbers. Being a probability function and being relative to all numbers it should probably add up to 100% then, or in the case of proportions which is what we have all should add up to 1. The problem is a histogram is a miserable way to figure that out. And clearly changing the bins from 20 to 50 not only changed the number of bins as we would expect it also changed the y-axis. Whaaaaaaa? As if to tell me that even though the data is the same the probability has changed. So how can i ever trust this?

Well, there is a way to figure out what is going on! I'm not going to lie, the first time i saw this my mind was a little blown. You can get all the data that is generated and used to create the histogram.

Pipe the results into a variable then simply display the variable. 



y<-hist(x$age,prob=TRUE,col="blue",breaks=10)
y

What you will see is the guts of what it takes to create the hist(); what we care about is the $counts, $density, and the $mids. Counts are the height of the bins, density is the actual probability and what will be the y axis, and mids is the x axis.

So, based on any probability we should get "1" indicating 100% of the data if we sum $density... Lets find out.



sum(y$density)
#[1] 0.2

I got .2...

Lets increase the bins and see what happens, we know the scale changed, maybe my density distribution will to. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

sum(y$density)
#[1] 1

Hmm, this time i get a "1". You will also notice that when the bins are increased to 50 the number of values in $mids and $density increased, it just so happens that for this dataset 50 was a better number of bins, though you will see that $density and $mids only went to a count of 42 values, which is enough.

With the below code you can get an estimation of the probability of specific numbers occurring. For the dataset i am using, 32.5 occurs 7.66% of the time, so that is the likely probability of that age occurring on future random variables. With less bins, you are basically getting an estimated average but not necessarily the full picture, so a density function in a histogram can be tricky and misleading if you attempt to make a decision on this. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

distz<- as.data.frame(list(z$density,z$mids))
names(distz) <- c("density","mids")
distz

So what is all of this? well, when you switch the hist() function to prob=true, you pretty much leave descriptive statistics and are now in probability. The thing that is used to figure out the distribution is called a kernel density estimation and in some cases called the Parzen-Rosenblatt-Window Density estimation, or kernel estimation. The least painful definition " to estimate a probability density function p(x) for a specific point p(x) from a sample p(xn) that doesn’t require any knowledge or assumption about the underlying distribution."

The definitions of the hist fields are int eh CRAN Help under hist() in the values section. Try this out, try different data and check out how the distribution changes with more or less bins.

Stats Stuff 6, Chebyshevs Rule

Published January 17, 2017 / by shep2010

Picking up from the last post we will now look at Chebyshevs rule. For this one we will be using ggplot2 histogram with annotations just to shake things up a bit.

Chebyshevs rule, theorem, inequality, whatever you want to call it states that all possible datasets regardless of shape will have 75% of the data within 2 standard deviations, and 88.89% within 3 standard deviations. This should apply to mound shaped datasets as well as bimodal (two mounds) and multimodal.

First, below is the empirical R code from the last blog post using ggplot2 if you are interested, otherwise skip this and move down. This is the script for the empirical rule calculations. Still using the US-Education.csv data. 


require(ggplot2)

usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)
str(usa)

highSchool <- subset(usa[c("FIPS.Code","Percent.of.adults.with.a.high.school.diploma.only..2010.2014")],FIPS.Code >0) 

#reanme the second column to something less annoying 
colnames(highSchool)[which(colnames(highSchool) == 'Percent.of.adults.with.a.high.school.diploma.only..2010.2014')] <- 'percent'


#create a variable with the mean and the standard devaiation 
hsMean <- mean(highSchool$percent,na.rm=TRUE)
hsSD <- sd(highSchool$percent,na.rm=TRUE)

#one standard deviation from the mean will "mean" one SD 
#to the left (-) of the mean and one SD to the right(+) of hte mean. 
oneSDleftRange <- (hsMean - hsSD)
oneSDrightRange <- (hsMean + hsSD)
oneSDleftRange;oneSDrightRange
oneSDrows <- nrow(subset(highSchool,percent > oneSDleftRange & percent < oneSDrightRange))
oneSDrows / nrow(highSchool)


#two standard deviations from the mean will "mean" two SDs 
#to the left (-) of the mean and two SDs to the right(+) of the mean. 
twoSDleftRange <- (hsMean - hsSD*2)
twoSDrightRange <- (hsMean + hsSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(highSchool,percent > twoSDleftRange & percent < twoSDrightRange))
twoSDrows / nrow(highSchool)

#two standard deviations from the mean will "mean" two SDs 
#to the left (-) of the mean and two SDs to the right(+) of the mean. 
threeSDleftRange <- (hsMean - hsSD*3)
threeSDrightRange <- (hsMean + hsSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(highSchool,percent > threeSDleftRange & percent < threeSDrightRange))
threeSDrows / nrow(highSchool)

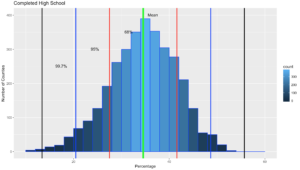
ggplot(data=highSchool, aes(highSchool$percent)) + 
  geom_histogram(breaks=seq(10, 60, by =2), 
                 col="blue", 
                 aes(fill=..count..))+
  labs(title="Completed High School") +
  labs(x="Percentage", y="Number of Counties") 

ggplot(data=highSchool, aes(highSchool$percent)) + 
  geom_histogram(breaks=seq(10, 60, by =2), 
                 col="blue", 
                 aes(fill=..count..))+
  labs(title="Completed High School") +
  labs(x="Percentage", y="Number of Counties") +
  geom_vline(xintercept=hsMean,colour="green",size=2)+
  geom_vline(xintercept=oneSDleftRange,colour="red",size=1)+
  geom_vline(xintercept=oneSDrightRange,colour="red",size=1)+
  geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
  geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
  geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
  geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
  annotate("text", x = hsMean+2, y = 401, label = "Mean")+
  annotate("text", x = oneSDleftRange+4, y = 351, label = "68%")+
  annotate("text", x = twoSDleftRange+4, y = 301, label = "95%")+
  annotate("text", x = threeSDleftRange+4, y = 251, label = "99.7%")

It would do no good to use the last dataset for to try out Chebyshevs rule as we know it is mond shaped, and fit oddly well to the empirical rule. Now lets try a different column in the US-Education dataset. 


usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)


ggplot(data=usa, aes(usa$X2013.Rural.urban.Continuum.Code)) + 
  geom_histogram(breaks=seq(1, 10, by =1), 
                 col="blue", 
                 aes(fill=..count..))

Comparatively speaking, this one looks a little funky, this is certainly bimodal, if not nearly trimodal. This should be a good test for Chebyshev.

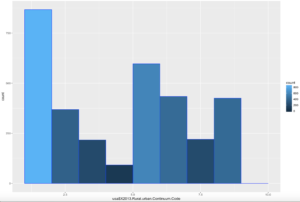
So, lets reuse some of the code above, drop the first standard dviation since Chebyshev does not need it and see if we can get this to work with "X2013.Rural.urban.Continuum.Code"




usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)
str(usa)

urbanMean <- mean(usa$X2013.Rural.urban.Continuum.Code,na.rm=TRUE)
urbanSD <- sd(usa$X2013.Rural.urban.Continuum.Code,na.rm=TRUE)


#two standard deviations from the mean will "mean" two SDs
#to the left (-) of the mean and two SDs to the right(+) of the mean.
twoSDleftRange <- (urbanMean - urbanSD*2)
twoSDrightRange <- (urbanMean + urbanSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(usa,X2013.Rural.urban.Continuum.Code > twoSDleftRange & usa$X2013.Rural.urban.Continuum.Code < twoSDrightRange))
twoSDrows / nrow(usa)

#two standard deviations from the mean will "mean" two SDs
#to the left (-) of the mean and two SDs to the right(+) of the mean.
threeSDleftRange <- (urbanMean - urbanSD*3)
threeSDrightRange <- (urbanMean + urbanSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(usa,X2013.Rural.urban.Continuum.Code > threeSDleftRange & X2013.Rural.urban.Continuum.Code < threeSDrightRange))
threeSDrows / nrow(usa)



ggplot(data=usa, aes(usa$X2013.Rural.urban.Continuum.Code)) + 
  geom_histogram(breaks=seq(1, 10, by =1), 
                 col="blue", 
                 aes(fill=..count..))+
                geom_vline(xintercept=urbanMean,colour="green",size=2)+
                geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
                geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
                geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
                geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
                annotate("text", x = urbanMean, y = 800, label = "Mean")+
                annotate("text", x = twoSDleftRange+1, y = 625, label = "68%")+
                annotate("text", x = threeSDleftRange+1.1, y = 425, label = "88.89%")

If you looked at the data and you looked at the range of two standard deviations above, you should know we have a problem; 98% of the data fell within 2 standard deviations. While yes, 68% of the data is also in the range it turns out this is a terrible example. The reason i include it is because it is just as important to see a test result that fails your expectation as it is for you to see on ethat is perfect! You will notice that the 3rd standard deviations is far outside the data range.

SO, what do we do? fake data to the rescue!

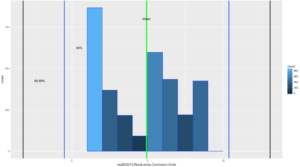
I try really hard to avoid using made up data because to me it makes no sense, where as car data, education data, population data, that all makes sense. But, there is no getting around it! Here is what you need to know, rnorm() generates random data based on a normal distribution using the variables standard deviation and a mean! But wait, we are trying to get multi-modal distribution. Then concatenate more than one normal distribution, eh? Lets try three.

We are going to test for one standard deviation just to see what it is, even though Chebyshevs rule has no interest in it, remember the rule states that 75% the data will fall within 2 standard deviations. 


#set.seed() will make sure the random number generation is not random everytime
set.seed(500)
x <- as.data.frame(c(rnorm(100,100,10)
                     ,(rnorm(100,400,20))
                     ,(rnorm(100,600,30))))

colnames(x) <- c("value")

#hist(x$value,nclass=100)
ggplot(data=x, aes(x$value)) + 
  geom_histogram( col="blue", 
                 aes(fill=..count..))

sd(x$value)    

mean(x$value)

#if you are interested in looking at just the first few values
head(x)



xMean <- mean(x$value)
xSD <- sd(x$value)


#one standard deviation from the mean will "mean" 1 * SD
#to the left (-) of the mean and one SD to the right(+) of the mean.
oneSDleftRange <- (xMean - xSD)
oneSDrightRange <- (xMean + xSD)
oneSDleftRange;oneSDrightRange
oneSDrows <- nrow(subset(x,value > oneSDleftRange & x < oneSDrightRange))
print("Data within One standard deviations");oneSDrows / nrow(x)


#two standard deviations from the mean will "mean" 2 * SD
#to the left (-) of the mean and two SDs to the right(+) of the mean.
twoSDleftRange <- (xMean - xSD*2)
twoSDrightRange <- (xMean + xSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(x,value > twoSDleftRange & x$value < twoSDrightRange))
print("Data within Two standard deviations");twoSDrows / nrow(x)


#three standard deviations from the mean will "mean" 3 * SD
#to the left (-) of the mean and two SDs to the right(+) of the mean.
threeSDleftRange <- (xMean - xSD*3)
threeSDrightRange <- (xMean + xSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(x,value > threeSDleftRange & x$value < threeSDrightRange))
print("Data within Three standard deviations");threeSDrows / nrow(x)

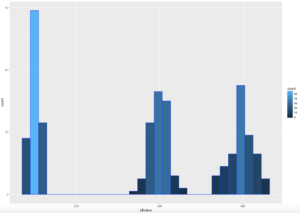
WOOHOO, Multimodal! Chebyshev said it works on anything, lets find out. The histogram below is a hot mess based on how the data was created, but it is clear that the empirical rule will not apply here, as the data is not mound shaped and is multimodal or trimodal.

Though Chebyshevs rule has no interest in 1 standard deviation i wanted to show it just so you could see what the 1 SD looks like. I challenge you to take the rnorm and see if you can modify the mean and SD parameters passed in to make it fall outside o the 75% of two standard deviations.

[1] "Data within One standard deviations" = 0.3966667 # or 39.66667%
[1] "Data within Two standard deviations" = 1 # or 100%
[1] "Data within Three standard deviations" = 1 or 100%

Lets add some lines; 



ggplot(data=x, aes(x$value)) + 
  geom_histogram( col="blue", 
                    aes(fill=..count..))+
                    geom_vline(xintercept=xMean,colour="green",size=2)+
                    geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
                    geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
                    geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
                    geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
                    annotate("text", x = xMean, y = 65, label = "Mean")+
                    annotate("text", x = twoSDleftRange+75, y = 50, label = "68%")+
                    annotate("text", x = threeSDleftRange+85, y = 40, label = "88.89%")

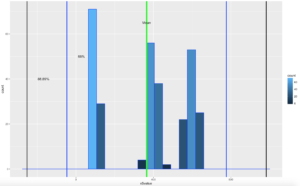
There you have it! It is becoming somewhat clear that based on the shape of the data and if you are using empirical or Chebyshevs rule, data falls into some very predictable patters, maybe from that we can make some predictions about new data coming in...?

Shep