Category Archives: histogram

Histogram in a little more detail.

Published January 20, 2017 / by shep2010

We have covered histograms in several posts so far and if you have been around the block a few times you probably decided it was a bar chart. Well, thats kinda true, the x axis is represented of the data, age n the x axis for instance would simply be age sorted ascending from left to right and the y axis for a frequency histogram would be the number of occurrences of that age. The most important option being the number of bins, everything else is just scale.

Load up some data and lets start by looking at the barchart versions of the histogram. 


install.packages("mosaicData")
install.packages("mosaic")

library("mosaic")
library("mosaicData")


data("HELPmiss")
View("HELPmiss")

str(HELPmiss)

x <- HELPmiss[c("age","anysub","cesd","drugrisk","sex","g1b","homeless","racegrp","substance")]

#the par command will allow you to show more than one plot side by side
#par(mfrow=c(2,2)); or par(mfrow=c(3,3)); etc...

par(mfrow=c(1,2))

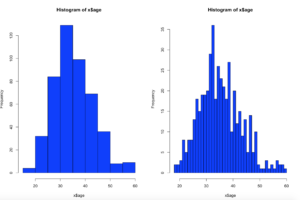
hist(x$age,col="blue",breaks=10)
hist(x$age,col="blue",breaks=50)

Using the code above you can see that the number of bins does change the graph too dramatically though some averaging clearly is taking place, but the x and y axis both make sense. We are basically looking at a bar chart, and based on shape we can derive some level of data distribution.

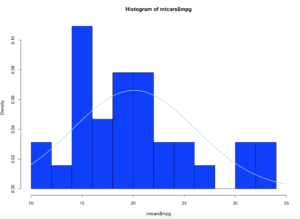
So, what happens when we add the line, the density curve, the PDF call it what you will? I have mentioned before it is a probability density function, but what does that really mean? And why do the numbers on the y axis charge so dramatically?

Well, first lets look at the code to create it. Same dataset as above, but lets add the "prob=TRUE" option. 



par(mfrow=c(1,2))
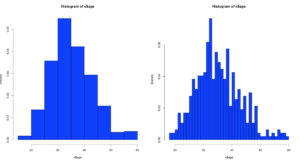
hist(x$age,prob=TRUE,col="blue",breaks=10)
hist(x$age,prob=TRUE,col="blue",breaks=50)

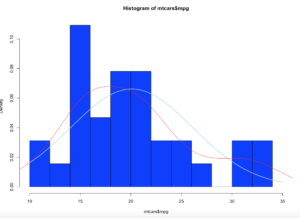
Notice the y axis scale is no longer frequency, but density. Okay, whats that? Density is a probability of that number occurring relative to all other numbers. Being a probability function and being relative to all numbers it should probably add up to 100% then, or in the case of proportions which is what we have all should add up to 1. The problem is a histogram is a miserable way to figure that out. And clearly changing the bins from 20 to 50 not only changed the number of bins as we would expect it also changed the y-axis. Whaaaaaaa? As if to tell me that even though the data is the same the probability has changed. So how can i ever trust this?

Well, there is a way to figure out what is going on! I'm not going to lie, the first time i saw this my mind was a little blown. You can get all the data that is generated and used to create the histogram.

Pipe the results into a variable then simply display the variable. 



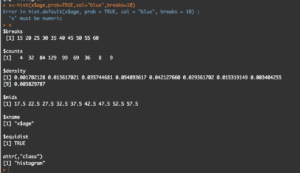
y<-hist(x$age,prob=TRUE,col="blue",breaks=10)
y

What you will see is the guts of what it takes to create the hist(); what we care about is the $counts, $density, and the $mids. Counts are the height of the bins, density is the actual probability and what will be the y axis, and mids is the x axis.

So, based on any probability we should get "1" indicating 100% of the data if we sum $density... Lets find out.



sum(y$density)
#[1] 0.2

I got .2...

Lets increase the bins and see what happens, we know the scale changed, maybe my density distribution will to. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

sum(y$density)
#[1] 1

Hmm, this time i get a "1". You will also notice that when the bins are increased to 50 the number of values in $mids and $density increased, it just so happens that for this dataset 50 was a better number of bins, though you will see that $density and $mids only went to a count of 42 values, which is enough.

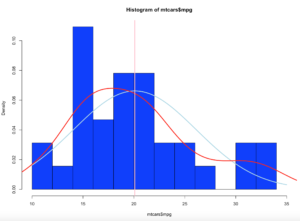
With the below code you can get an estimation of the probability of specific numbers occurring. For the dataset i am using, 32.5 occurs 7.66% of the time, so that is the likely probability of that age occurring on future random variables. With less bins, you are basically getting an estimated average but not necessarily the full picture, so a density function in a histogram can be tricky and misleading if you attempt to make a decision on this. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

distz<- as.data.frame(list(z$density,z$mids))
names(distz) <- c("density","mids")
distz

So what is all of this? well, when you switch the hist() function to prob=true, you pretty much leave descriptive statistics and are now in probability. The thing that is used to figure out the distribution is called a kernel density estimation and in some cases called the Parzen-Rosenblatt-Window Density estimation, or kernel estimation. The least painful definition " to estimate a probability density function p(x) for a specific point p(x) from a sample p(xn) that doesn’t require any knowledge or assumption about the underlying distribution."

The definitions of the hist fields are int eh CRAN Help under hist() in the values section. Try this out, try different data and check out how the distribution changes with more or less bins.

Stats Stuff 4, Variance and Standard Deviation

Published January 10, 2017 / by shep2010

It is said by someone that standard deviation and variance are tedious to calculate by hand, I would agree with that but it is likely you will never ever do any of this by hand. That was more likely the stats of years gone by. But, in R you only have to know two commands to achieve standard deviation and variance, sd() and var(). Bam we are done! Okay one more, in SQL Server the commands are stdev and var! Bam, we are done!

Fine! Here is my frustration with all of this, exactly what is it? My intro to stats class took 50 slides for this part and only two of them made sense, the two with words, the other 48 were an x,y grid, not helpful at all.

Variance is the expected value of the squared deviation of a random variable for its mean. Looking at the R formula is easier. Variance = sum((x – mean(x)) ^2 ) / (length(x)-1). Work your way from the inside of the formula out of you need to.

Standard deviation is a measure of the variation of dispersion of the data. This has a nice easy formula as well, and it is based on variance. Standard Deviation = sqrt(sum((x – mean(x)) ^2 ) / (length(x)-1)). It’s the square root of the variance, how cool is that, you only need to know one formula!

Just to get started, here is a short and simple demo of both formulas and the R function;



#Load up a vector with some numbers
x<- c(1,2,3,5,8)

#This is the long hand of variance
#hopefully, the formula will produce the same results as var()
sum((x - mean(x)) ^2 ) / (length(x)-1)

var(x)

#This is the long hand of standard deviation
#Notica that it is the square root of variance formula 
#hopefully, the formula will produce the same results as var()
sqrt(sum((x - mean(x)) ^2 ) / (length(x)-1))

#you could also just use the square root of the output of var()
sqrt(var(x))

#or just run sd()
sd(x)

In the long hand formula, did you notice we are taking the length of x and subtracting 1 for both sd and var? Do you know why? Blame Fred Bessel, he died in 1846 so i don't think there is much chance of getting around this. Its Bessels correction, it is unique to a sample except that all statistical software will use the correction by default even if you are using an entire population. It is stated that this is used when the population mean is unknown. Though you will notice regardless if you or i know the population it is computed as if we do not, get used to it, n-1 is built into every software, the de facto standard.

I am going to cover normal distribution in the next couple of blog posts, but lets make a hot mess of the mtcars$mpg data first.

Lets get a histogram first; 



hist(mtcars$mpg,col="blue",breaks=15,freq=FALSE,xlim=c(10,35))





curve(dnorm(x, mean=mean(mtcars$mpg), sd=sd(mtcars$mpg)), col="lightblue",add=TRUE, lwd=2)

Brace yourself, i am going to use as few effective words as possible to describe what curve() and dnorm() did. Looking at at the blue line; what we have now is a PDF, probability density function line. What this means is, since the norm took in the standard deviation and the mean it creates a line density line to try an predict where a new piece of incoming data is likely to fall.

Add a line



lines(density(mtcars$mpg),col="red")

Looking at the red line, this is a kernel density estimate plot layer over the histogram, this basically smoothes the da based on the sample provided. We may get deeper into this way later, as this is pretty advanced. Bu notice how it models the underlying data.

Lets add a mean line in Pink



abline(v = mean(mtcars$mpg),col = "pink",lwd = 3)

The mean as you will recall is the average of the values in mtcars$mpg.

Much more on this very soon, this si a good setup for normal distribution, and the empirical rule.

Shep