Monthly Archives: January 2017

Histogram in a little more detail.

Published January 20, 2017 / by shep2010

We have covered histograms in several posts so far and if you have been around the block a few times you probably decided it was a bar chart. Well, thats kinda true, the x axis is represented of the data, age n the x axis for instance would simply be age sorted ascending from left to right and the y axis for a frequency histogram would be the number of occurrences of that age. The most important option being the number of bins, everything else is just scale.

Load up some data and lets start by looking at the barchart versions of the histogram. 


install.packages("mosaicData")
install.packages("mosaic")

library("mosaic")
library("mosaicData")


data("HELPmiss")
View("HELPmiss")

str(HELPmiss)

x <- HELPmiss[c("age","anysub","cesd","drugrisk","sex","g1b","homeless","racegrp","substance")]

#the par command will allow you to show more than one plot side by side
#par(mfrow=c(2,2)); or par(mfrow=c(3,3)); etc...

par(mfrow=c(1,2))

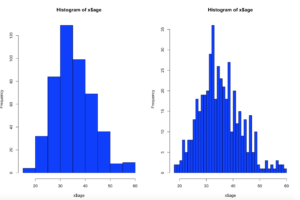
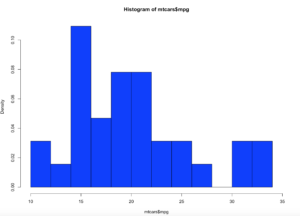
hist(x$age,col="blue",breaks=10)
hist(x$age,col="blue",breaks=50)

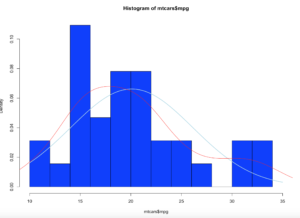
Using the code above you can see that the number of bins does change the graph too dramatically though some averaging clearly is taking place, but the x and y axis both make sense. We are basically looking at a bar chart, and based on shape we can derive some level of data distribution.

So, what happens when we add the line, the density curve, the PDF call it what you will? I have mentioned before it is a probability density function, but what does that really mean? And why do the numbers on the y axis charge so dramatically?

Well, first lets look at the code to create it. Same dataset as above, but lets add the "prob=TRUE" option. 



par(mfrow=c(1,2))
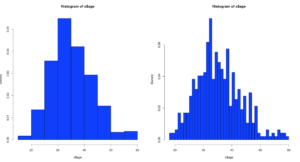
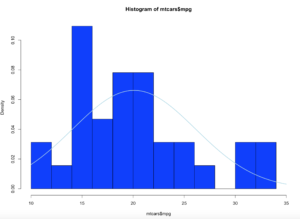
hist(x$age,prob=TRUE,col="blue",breaks=10)
hist(x$age,prob=TRUE,col="blue",breaks=50)

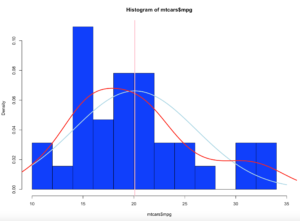
Notice the y axis scale is no longer frequency, but density. Okay, whats that? Density is a probability of that number occurring relative to all other numbers. Being a probability function and being relative to all numbers it should probably add up to 100% then, or in the case of proportions which is what we have all should add up to 1. The problem is a histogram is a miserable way to figure that out. And clearly changing the bins from 20 to 50 not only changed the number of bins as we would expect it also changed the y-axis. Whaaaaaaa? As if to tell me that even though the data is the same the probability has changed. So how can i ever trust this?

Well, there is a way to figure out what is going on! I'm not going to lie, the first time i saw this my mind was a little blown. You can get all the data that is generated and used to create the histogram.

Pipe the results into a variable then simply display the variable. 



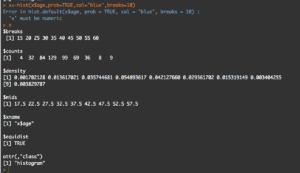
y<-hist(x$age,prob=TRUE,col="blue",breaks=10)
y

What you will see is the guts of what it takes to create the hist(); what we care about is the $counts, $density, and the $mids. Counts are the height of the bins, density is the actual probability and what will be the y axis, and mids is the x axis.

So, based on any probability we should get "1" indicating 100% of the data if we sum $density... Lets find out.



sum(y$density)
#[1] 0.2

I got .2...

Lets increase the bins and see what happens, we know the scale changed, maybe my density distribution will to. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

sum(y$density)
#[1] 1

Hmm, this time i get a "1". You will also notice that when the bins are increased to 50 the number of values in $mids and $density increased, it just so happens that for this dataset 50 was a better number of bins, though you will see that $density and $mids only went to a count of 42 values, which is enough.

With the below code you can get an estimation of the probability of specific numbers occurring. For the dataset i am using, 32.5 occurs 7.66% of the time, so that is the likely probability of that age occurring on future random variables. With less bins, you are basically getting an estimated average but not necessarily the full picture, so a density function in a histogram can be tricky and misleading if you attempt to make a decision on this. 



z<-hist(x$age,prob=TRUE,col="blue",breaks=50)
z

distz<- as.data.frame(list(z$density,z$mids))
names(distz) <- c("density","mids")
distz

So what is all of this? well, when you switch the hist() function to prob=true, you pretty much leave descriptive statistics and are now in probability. The thing that is used to figure out the distribution is called a kernel density estimation and in some cases called the Parzen-Rosenblatt-Window Density estimation, or kernel estimation. The least painful definition " to estimate a probability density function p(x) for a specific point p(x) from a sample p(xn) that doesn’t require any knowledge or assumption about the underlying distribution."

The definitions of the hist fields are int eh CRAN Help under hist() in the values section. Try this out, try different data and check out how the distribution changes with more or less bins.

Stats Stuff 6, Chebyshevs Rule

Published January 17, 2017 / by shep2010

Picking up from the last post we will now look at Chebyshevs rule. For this one we will be using ggplot2 histogram with annotations just to shake things up a bit.

Chebyshevs rule, theorem, inequality, whatever you want to call it states that all possible datasets regardless of shape will have 75% of the data within 2 standard deviations, and 88.89% within 3 standard deviations. This should apply to mound shaped datasets as well as bimodal (two mounds) and multimodal.

First, below is the empirical R code from the last blog post using ggplot2 if you are interested, otherwise skip this and move down. This is the script for the empirical rule calculations. Still using the US-Education.csv data. 


require(ggplot2)

usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)
str(usa)

highSchool <- subset(usa[c("FIPS.Code","Percent.of.adults.with.a.high.school.diploma.only..2010.2014")],FIPS.Code >0) 

#reanme the second column to something less annoying 
colnames(highSchool)[which(colnames(highSchool) == 'Percent.of.adults.with.a.high.school.diploma.only..2010.2014')] <- 'percent'


#create a variable with the mean and the standard devaiation 
hsMean <- mean(highSchool$percent,na.rm=TRUE)
hsSD <- sd(highSchool$percent,na.rm=TRUE)

#one standard deviation from the mean will "mean" one SD 
#to the left (-) of the mean and one SD to the right(+) of hte mean. 
oneSDleftRange <- (hsMean - hsSD)
oneSDrightRange <- (hsMean + hsSD)
oneSDleftRange;oneSDrightRange
oneSDrows <- nrow(subset(highSchool,percent > oneSDleftRange & percent < oneSDrightRange))
oneSDrows / nrow(highSchool)


#two standard deviations from the mean will "mean" two SDs 
#to the left (-) of the mean and two SDs to the right(+) of the mean. 
twoSDleftRange <- (hsMean - hsSD*2)
twoSDrightRange <- (hsMean + hsSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(highSchool,percent > twoSDleftRange & percent < twoSDrightRange))
twoSDrows / nrow(highSchool)

#two standard deviations from the mean will "mean" two SDs 
#to the left (-) of the mean and two SDs to the right(+) of the mean. 
threeSDleftRange <- (hsMean - hsSD*3)
threeSDrightRange <- (hsMean + hsSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(highSchool,percent > threeSDleftRange & percent < threeSDrightRange))
threeSDrows / nrow(highSchool)

ggplot(data=highSchool, aes(highSchool$percent)) + 
  geom_histogram(breaks=seq(10, 60, by =2), 
                 col="blue", 
                 aes(fill=..count..))+
  labs(title="Completed High School") +
  labs(x="Percentage", y="Number of Counties") 

ggplot(data=highSchool, aes(highSchool$percent)) + 
  geom_histogram(breaks=seq(10, 60, by =2), 
                 col="blue", 
                 aes(fill=..count..))+
  labs(title="Completed High School") +
  labs(x="Percentage", y="Number of Counties") +
  geom_vline(xintercept=hsMean,colour="green",size=2)+
  geom_vline(xintercept=oneSDleftRange,colour="red",size=1)+
  geom_vline(xintercept=oneSDrightRange,colour="red",size=1)+
  geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
  geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
  geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
  geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
  annotate("text", x = hsMean+2, y = 401, label = "Mean")+
  annotate("text", x = oneSDleftRange+4, y = 351, label = "68%")+
  annotate("text", x = twoSDleftRange+4, y = 301, label = "95%")+
  annotate("text", x = threeSDleftRange+4, y = 251, label = "99.7%")

It would do no good to use the last dataset for to try out Chebyshevs rule as we know it is mond shaped, and fit oddly well to the empirical rule. Now lets try a different column in the US-Education dataset. 


usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)


ggplot(data=usa, aes(usa$X2013.Rural.urban.Continuum.Code)) + 
  geom_histogram(breaks=seq(1, 10, by =1), 
                 col="blue", 
                 aes(fill=..count..))

Comparatively speaking, this one looks a little funky, this is certainly bimodal, if not nearly trimodal. This should be a good test for Chebyshev.

So, lets reuse some of the code above, drop the first standard dviation since Chebyshev does not need it and see if we can get this to work with "X2013.Rural.urban.Continuum.Code"




usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)
str(usa)

urbanMean <- mean(usa$X2013.Rural.urban.Continuum.Code,na.rm=TRUE)
urbanSD <- sd(usa$X2013.Rural.urban.Continuum.Code,na.rm=TRUE)


#two standard deviations from the mean will "mean" two SDs
#to the left (-) of the mean and two SDs to the right(+) of the mean.
twoSDleftRange <- (urbanMean - urbanSD*2)
twoSDrightRange <- (urbanMean + urbanSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(usa,X2013.Rural.urban.Continuum.Code > twoSDleftRange & usa$X2013.Rural.urban.Continuum.Code < twoSDrightRange))
twoSDrows / nrow(usa)

#two standard deviations from the mean will "mean" two SDs
#to the left (-) of the mean and two SDs to the right(+) of the mean.
threeSDleftRange <- (urbanMean - urbanSD*3)
threeSDrightRange <- (urbanMean + urbanSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(usa,X2013.Rural.urban.Continuum.Code > threeSDleftRange & X2013.Rural.urban.Continuum.Code < threeSDrightRange))
threeSDrows / nrow(usa)



ggplot(data=usa, aes(usa$X2013.Rural.urban.Continuum.Code)) + 
  geom_histogram(breaks=seq(1, 10, by =1), 
                 col="blue", 
                 aes(fill=..count..))+
                geom_vline(xintercept=urbanMean,colour="green",size=2)+
                geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
                geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
                geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
                geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
                annotate("text", x = urbanMean, y = 800, label = "Mean")+
                annotate("text", x = twoSDleftRange+1, y = 625, label = "68%")+
                annotate("text", x = threeSDleftRange+1.1, y = 425, label = "88.89%")

If you looked at the data and you looked at the range of two standard deviations above, you should know we have a problem; 98% of the data fell within 2 standard deviations. While yes, 68% of the data is also in the range it turns out this is a terrible example. The reason i include it is because it is just as important to see a test result that fails your expectation as it is for you to see on ethat is perfect! You will notice that the 3rd standard deviations is far outside the data range.

SO, what do we do? fake data to the rescue!

I try really hard to avoid using made up data because to me it makes no sense, where as car data, education data, population data, that all makes sense. But, there is no getting around it! Here is what you need to know, rnorm() generates random data based on a normal distribution using the variables standard deviation and a mean! But wait, we are trying to get multi-modal distribution. Then concatenate more than one normal distribution, eh? Lets try three.

We are going to test for one standard deviation just to see what it is, even though Chebyshevs rule has no interest in it, remember the rule states that 75% the data will fall within 2 standard deviations. 


#set.seed() will make sure the random number generation is not random everytime
set.seed(500)
x <- as.data.frame(c(rnorm(100,100,10)
                     ,(rnorm(100,400,20))
                     ,(rnorm(100,600,30))))

colnames(x) <- c("value")

#hist(x$value,nclass=100)
ggplot(data=x, aes(x$value)) + 
  geom_histogram( col="blue", 
                 aes(fill=..count..))

sd(x$value)    

mean(x$value)

#if you are interested in looking at just the first few values
head(x)



xMean <- mean(x$value)
xSD <- sd(x$value)


#one standard deviation from the mean will "mean" 1 * SD
#to the left (-) of the mean and one SD to the right(+) of the mean.
oneSDleftRange <- (xMean - xSD)
oneSDrightRange <- (xMean + xSD)
oneSDleftRange;oneSDrightRange
oneSDrows <- nrow(subset(x,value > oneSDleftRange & x < oneSDrightRange))
print("Data within One standard deviations");oneSDrows / nrow(x)


#two standard deviations from the mean will "mean" 2 * SD
#to the left (-) of the mean and two SDs to the right(+) of the mean.
twoSDleftRange <- (xMean - xSD*2)
twoSDrightRange <- (xMean + xSD*2)
twoSDleftRange;twoSDrightRange
twoSDrows <- nrow(subset(x,value > twoSDleftRange & x$value < twoSDrightRange))
print("Data within Two standard deviations");twoSDrows / nrow(x)


#three standard deviations from the mean will "mean" 3 * SD
#to the left (-) of the mean and two SDs to the right(+) of the mean.
threeSDleftRange <- (xMean - xSD*3)
threeSDrightRange <- (xMean + xSD*3)
threeSDleftRange;threeSDrightRange
threeSDrows <- nrow(subset(x,value > threeSDleftRange & x$value < threeSDrightRange))
print("Data within Three standard deviations");threeSDrows / nrow(x)

WOOHOO, Multimodal! Chebyshev said it works on anything, lets find out. The histogram below is a hot mess based on how the data was created, but it is clear that the empirical rule will not apply here, as the data is not mound shaped and is multimodal or trimodal.

Though Chebyshevs rule has no interest in 1 standard deviation i wanted to show it just so you could see what the 1 SD looks like. I challenge you to take the rnorm and see if you can modify the mean and SD parameters passed in to make it fall outside o the 75% of two standard deviations.

[1] "Data within One standard deviations" = 0.3966667 # or 39.66667%
[1] "Data within Two standard deviations" = 1 # or 100%
[1] "Data within Three standard deviations" = 1 or 100%

Lets add some lines; 



ggplot(data=x, aes(x$value)) + 
  geom_histogram( col="blue", 
                    aes(fill=..count..))+
                    geom_vline(xintercept=xMean,colour="green",size=2)+
                    geom_vline(xintercept=twoSDleftRange,colour="blue",size=1)+
                    geom_vline(xintercept=twoSDrightRange,colour="blue",size=1)+
                    geom_vline(xintercept=threeSDleftRange,colour="black",size=1)+
                    geom_vline(xintercept=threeSDrightRange,colour="black",size=1)+
                    annotate("text", x = xMean, y = 65, label = "Mean")+
                    annotate("text", x = twoSDleftRange+75, y = 50, label = "68%")+
                    annotate("text", x = threeSDleftRange+85, y = 40, label = "88.89%")

There you have it! It is becoming somewhat clear that based on the shape of the data and if you are using empirical or Chebyshevs rule, data falls into some very predictable patters, maybe from that we can make some predictions about new data coming in...?

Shep

Stats Stuff 5, Normal Distribution, Empirical Rule

Published January 13, 2017 / by shep2010

So, we have covered standard deviation and mean, discussed central tendency, and we have demonstrated some histograms. You are familiar with what a histogram looks like and that depending on the data, it can take many shapes. Today we are going to discuss distribution that specifically applies to mound shaped data. We happen to have been working with a couple of datasets that meet this criteria perfectly, or at least it does in shape.

In the last blog, we had two datasets from US Educational attainment that appeared to be mound shaped, that being the key word, mound shaped. If it is mound shaped, we should be able to make some predictions about the data using the Empirical Rule, and if not mound shape, the Chebyshevs rule.

The point of this as stated in my stats class, to link visualization of distributions to numerical measures of center and location. This will only apply to mound shaped data, like the following;

When someone says mound shaped data, this is the text book example of mound shaped. This is from the US-Education.csv data that we have been playing with, below are the commands to get you started and get you a histogram.

Just so you fully understand wha this data is, every person in the US reports their level of educational attainment to the Census every ten years, every few years this data is updated and projected to estimate reasonably current values. This we will be using is for the 2010-2014 years which is the five year average compiled by the American Community Survey. I highly encourage use of this website for test data, all of it has to be manipulated a little bit, but it typically takes minutes to get it into a format R can use. 


usa <- read.csv("/data/US-Education.csv",stringsAsFactors=FALSE)
str(usa)

#While not required, i want to isolate the data we will be working with 
highSchool <- subset(usa[c("FIPS.Code","Percent.of.adults.with.a.high.school.diploma.only..2010.2014")],FIPS.Code >0) 

#reanme the second column to something less annoying 
colnames(highSchool)[which(colnames(highSchool) == 'Percent.of.adults.with.a.high.school.diploma.only..2010.2014')] <- 'percent'

#Display a histogram 
hist(highSchool$percent
    ,xlim=c(5,60)
    ,breaks=20
    ,xlab = "Percent Completed High School "
    ,ylab = "Number of Counties"
    ,main = ""
    ,col = "lightblue")

The Empirical rule states that

68% of the data will fall with in 1 standard deviation of the mean,
95% of the data will fall within 2 standard deviations of the mean, and
99.7% of the data will fall within 3 standard deviations of them mean.

Lets find out! 


#create a variable with the mean and the standard devaiation 
hsMean <- mean(highSchool$percent,na.rm=TRUE)
hsSD <- sd(highSchool$percent,na.rm=TRUE)

#one standard deviation from the mean will "mean" one SD 
#to the left (-) of the mean and one SD to the right(+) of the mean. 
#lets calculate and store them
 
oneSDleftRange <- (hsMean - hsSD)
oneSDrightRange <- (hsMean + hsSD)

oneSDleftRange;oneSDrightRange


##[1] 27.51472 is one sd to the left of the mean
##[1] 41.60826 is one sd to the right of the mean

#lets calculate the number of rows that fall 
#between 27.51472(oneSDleftRange) and 41.60826(oneSDrightRange)
oneSDrows <- nrow(subset(highSchool,percent > oneSDleftRange & percent < oneSDrightRange))

# whats the percentage?
oneSDrows / nrow(highSchool)

If everything worked properly, you should have seen that the percentage of counties within one standard deviation of the mean is "0.6803778" or 68.04%. Wel that was kinda creepy wasn't it? The empirical rule states that 68% of the data will be within one standard deviation.

Lets keep going. 


#two standard deviations from the mean will "mean" two SDs 
#to the left (-) of the mean and two SDs to the right(+) of the mean. 
twoSDleftRange <- (hsMean - hsSD*2)
twoSDrightRange <- (hsMean + hsSD*2)


twoSDleftRange;twoSDrightRange

##[1] 20.46795 is two sds to the left of the mean
##[1] 48.65503 is two sds to the right of the mean

twoSDrows <- nrow(subset(highSchool,percent > twoSDleftRange & percent < twoSDrightRange))

twoSDrows / nrow(highSchool)

If your math is the same as my math, you should have gotten 95.09%, so far the empirical rule is holding...

What about three standard deviations? 


threeSDleftRange <- (hsMean - hsSD*3)
threeSDrightRange <- (hsMean + hsSD*3)

threeSDleftRange;threeSDrightRange

threeSDrows <- nrow(subset(highSchool,percent > threeSDleftRange & percent < threeSDrightRange))

threeSDrows / nrow(highSchool)

99.32% at three standard deviations, its like the empirical rule knows our data! Before we move on, lets add some lines... 


hist(highSchool$percent
     ,xlim=c(5,60)
     ,breaks=20
     ,xlab = "Percent Completed High School "
     ,ylab = "Number of Counties"
     ,main = ""
     ,col = "lightblue")

abline(v = threeSDleftRange,col = "black",lwd = 3)
abline(v = threeSDrightRange,col = "black",lwd = 3)

abline(v = twoSDleftRange,col = "royalblue",lwd = 3)
abline(v = twoSDrightRange,col = "royalblue",lwd = 3)

abline(v = oneSDleftRange,col = "red",lwd = 3)
abline(v = oneSDrightRange,col = "red",lwd = 3)

abline(v = hsMean,col = "green",lwd = 4)


legend(x="topright",
       c("Mean","3 SDs 99.7%", "2 SDs 95%", "1 SD 68%"),
       col = c("Green","black", "royalblue", "red"),
       lwd = c(2, 2, 2),
       cex=0.75
       )

You can see the distribution of the data below, it really does seem to fall into pretty predictable standard deviations.

It has frequently been my opinion and others that R was written by an angry teenager to get even with his boomer parents, while not entirely true R has many frustrations. The nice thing is, you can write your own package to handle many of these more complex visualizations, i stuck to Base R for this histogram, and it does get the point across, but ggplot provides much better graphics and legends.

More Chebyshev in the next post!

Shep

R Markdown

Published January 11, 2017 / by shep2010

This is a slight diversion into a tool built into R called R Markdown, and Shiny will be coming up in a few days. Why is this important? It gives you a living document you can add text and r scripts to to produce just the output from R. I wrote my Stats grad project using just R Markdown and saved it to a PDF, no Word or open office tools.

Its a mix of HTML and R, so if you know a tiny bit about HTML programing you will be fine, otherwise, use the R Markdown Cheat sheet and Reference Guide which i just annoyingly found out existed…

I am going to give you a full R Markdown document to get you started.

Create a new R Markdown file;

Then Run it by selecting the “Knit” drop down in the middle left of the toolbar and selecting Knit to HTML.

This will create an html document that you can open in a browser, it comes with some default mtcars data just so you can see some output. Try out some R commands and doodle around a bit before starting the code below. This is the file data file we will be using, US-Education.csv It contains just the 2010-2014 educational attainment estimates per count in the US.

In the code books below i will put in each section of the R Markdown and discuss it, each R code block can me moved to r console to be run.

The first section Is the title that will show up on the top of the doc, copy this into the markdown file and run it by itself. I am using an html style tag as i want some of the plots to be two columns across.

You will also see the first R command in an “R” block identified by ““`{r} and terminated with ““`”. Feel free to remove options and change options to see what happens.

Notice below the style tag is wrong, when you copy it out you will need to put the “<" back in from of the style tag. If i format it correctly wordpress takes it as an internal style tag to this post. 


---
title: "Educational Attainment by County"

output: html_document
---

style>
  .col2 {
    columns: 2 200px;         /* number of columns and width in pixels*/
    -webkit-columns: 2 200px; /* chrome, safari */
    -moz-columns: 2 200px;    /* firefox */
     line-height: 2em;
     font-size: 10pt;

  }

/style>

```{r setup, include=FALSE}
knitr::opts_chunk$set(echo = FALSE,warning=FALSE)

#require is the fancy version of install package/library
require(choroplethr)

```

This will be the next section in the markup, load a dataframe for each of the four educational attainment categories. 


```{r one}

#Load data
 setwd("/data/")
 usa <- read.csv("US-Education.csv",stringsAsFactors=FALSE)

#Seperate data for choropleth 
 lessHighSchool <- subset(usa[c("FIPS.Code","Percent.of.adults.with.less.than.a.high.school.diploma..2010.2014")],FIPS.Code >0)
 
highSchool <- subset(usa[c("FIPS.Code","Percent.of.adults.with.a.high.school.diploma.only..2010.2014")],FIPS.Code >0) 
 
someCollege <- subset(usa[c("FIPS.Code","Percent.of.adults.completing.some.college.or.associate.s.degree..2010.2014")],FIPS.Code >0)
 
college <- subset(usa[c("FIPS.Code","Percent.of.adults.with.a.bachelor.s.degree.or.higher..2010.2014")],FIPS.Code >0)

#rename columns for Choropleth
 
 colnames(lessHighSchool)[which(colnames(lessHighSchool) == 'FIPS.Code')] <- 'region'
 
 colnames(lessHighSchool)[which(colnames(lessHighSchool) == 'Percent.of.adults.with.less.than.a.high.school.diploma..2010.2014')] <- 'value'

# 
# or
#
 names(highSchool) <-c("region","value")
 names(someCollege) <-c("region","value")
 names(college) <-c("region","value")
 
 
```

The next section will create four histograms of the college attainment by category. Notice the distribution of the data, normal distribution, right skew, left skew, bimodal? We will discuss them next blog.

Notice for the next section i have the "div" without the left "<", be sure to put those back. 



div class="col2">

```{r Histogram 1}
 hist(lessHighSchool$value,xlim=c(0,60),breaks=30, xlab = "Percent of High School Dropouts", ylab="Number of Counties",main="",col="lightblue")


 hist(highSchool$value,xlim=c(0,60),breaks=30, xlab = "Percent Completed High School ", ylab="Number of Counties",main="",col="lightblue")
 
```
 
 
```{r Histogram 2}

 hist(someCollege$value,xlim=c(0,50),breaks=30, xlab = "Percent Completed Associates or Some College ", ylab="Number of Counties",main="",col="lightblue")
 
 hist(college$value,xlim=c(0,90),breaks=30, xlab = "Percent Completed Bachelors Degree or Higher ", ylab="Number of Counties",main="",col="lightblue")


```

/div>

The next section is the choropleth, for the high school dropouts, notice the R chunk parameters to size the plot area. 



```{r two, fig.width=9, fig.height=5, fig.align='right'}


 county_choropleth(lessHighSchool,
                  
                   title = "Proportion of High School Dropouts",
                   legend="Proportion",
                   num_colors=9)
 
```

There are three more choropleths that you will have to do on your own! you have the data, and the syntax. If you have trouble with this, the red file i used is here Education.rmd

In the end, you should have a histogram looking like this;

And if you make it to the first choropleth, Percentage that did not complete high school;

Stats Stuff 4, Variance and Standard Deviation

Published January 10, 2017 / by shep2010

It is said by someone that standard deviation and variance are tedious to calculate by hand, I would agree with that but it is likely you will never ever do any of this by hand. That was more likely the stats of years gone by. But, in R you only have to know two commands to achieve standard deviation and variance, sd() and var(). Bam we are done! Okay one more, in SQL Server the commands are stdev and var! Bam, we are done!

Fine! Here is my frustration with all of this, exactly what is it? My intro to stats class took 50 slides for this part and only two of them made sense, the two with words, the other 48 were an x,y grid, not helpful at all.

Variance is the expected value of the squared deviation of a random variable for its mean. Looking at the R formula is easier. Variance = sum((x – mean(x)) ^2 ) / (length(x)-1). Work your way from the inside of the formula out of you need to.

Standard deviation is a measure of the variation of dispersion of the data. This has a nice easy formula as well, and it is based on variance. Standard Deviation = sqrt(sum((x – mean(x)) ^2 ) / (length(x)-1)). It’s the square root of the variance, how cool is that, you only need to know one formula!

Just to get started, here is a short and simple demo of both formulas and the R function;



#Load up a vector with some numbers
x<- c(1,2,3,5,8)

#This is the long hand of variance
#hopefully, the formula will produce the same results as var()
sum((x - mean(x)) ^2 ) / (length(x)-1)

var(x)

#This is the long hand of standard deviation
#Notica that it is the square root of variance formula 
#hopefully, the formula will produce the same results as var()
sqrt(sum((x - mean(x)) ^2 ) / (length(x)-1))

#you could also just use the square root of the output of var()
sqrt(var(x))

#or just run sd()
sd(x)

In the long hand formula, did you notice we are taking the length of x and subtracting 1 for both sd and var? Do you know why? Blame Fred Bessel, he died in 1846 so i don't think there is much chance of getting around this. Its Bessels correction, it is unique to a sample except that all statistical software will use the correction by default even if you are using an entire population. It is stated that this is used when the population mean is unknown. Though you will notice regardless if you or i know the population it is computed as if we do not, get used to it, n-1 is built into every software, the de facto standard.

I am going to cover normal distribution in the next couple of blog posts, but lets make a hot mess of the mtcars$mpg data first.

Lets get a histogram first; 



hist(mtcars$mpg,col="blue",breaks=15,freq=FALSE,xlim=c(10,35))





curve(dnorm(x, mean=mean(mtcars$mpg), sd=sd(mtcars$mpg)), col="lightblue",add=TRUE, lwd=2)

Brace yourself, i am going to use as few effective words as possible to describe what curve() and dnorm() did. Looking at at the blue line; what we have now is a PDF, probability density function line. What this means is, since the norm took in the standard deviation and the mean it creates a line density line to try an predict where a new piece of incoming data is likely to fall.

Add a line



lines(density(mtcars$mpg),col="red")

Looking at the red line, this is a kernel density estimate plot layer over the histogram, this basically smoothes the da based on the sample provided. We may get deeper into this way later, as this is pretty advanced. Bu notice how it models the underlying data.

Lets add a mean line in Pink



abline(v = mean(mtcars$mpg),col = "pink",lwd = 3)

The mean as you will recall is the average of the values in mtcars$mpg.

Much more on this very soon, this si a good setup for normal distribution, and the empirical rule.

Shep

Stats Stuff 3, Range, IQR

Published January 9, 2017 / by shep2010

The next topics (Range, IQR, Variance and Standard Deviation) took up a combined 120 power point slides in my stats class, which means that describing all in a single post will not happen, and maybe two posts minimum, but I will try to keep it under 120 slides or pages.

So, range, IQR (Interquartile Range), variance and standard deviation fall under summary measures as ways to describe numerical data.

Range – is the measure of dispersion or spread. Using central tendency methods we can see where most of the data is piled up, but what do we know about the variability of the data? The range of the data is basically the maximum value – the minimum value.

What to know about range? It is sensitive to outliers. It is unconcerned about the distribution of the data in the set.

For instance, if I had a hybrid car in my mtcars dataset that achieved 120 mpg by the petrol standards set forth by the EPA, my range for mpg would be 10.40mpg to 120mpg. If I told you the cars in my sample had a mpg range of 10.40mpg to 120mpg what would you think of the cars? What range fails to disclose is that the next highest mpg car is 33.9, that’s pretty far away and not all representative of the true dataset.

Run the following, try it out on your own data sets.


data(mtcars)
View(mtcars)

range(mtcars$mpg)
range(mtcars$wt)
range(mtcars$hp)

# if you are old school hard core, 
# "c" is to concatenate the results. 

c(min(mtcars$hp),max(mtcars$hp))

Interquartile Range – since we have already discussed quartiles this one is easy, the inter-quartile-range is simply the middle 50%, the values that reside between the 1st quartile(25%) and the first 3rd(75%) quartile. Summary() and favstats will give us the min(0%), Q1, Q2, Q3, max (100%)as will quantile().


quantile(mtcars$mpg)
summary(mtcars$mpg)
favstats(mtcars$mpg)

IQRs help us find Outlier which is an observation point that is distant from other observations. An outlier may be due to variability in the measurement or it may indicate experimental error; the latter are sometimes excluded from the data set.

One of the techniques for removing outliers is to use the IQR to isolate the center 50% of the data. Lets use the Florida dataset from the scatterplot blog and see how the plot changes.

I am going to demonstrate the way i know to do this. Understand this is a method to perform this task, two years from now i will probably think this is amateuresque, but until then here we go.

We will need the first quintile and the third quantile and then subtract one from the other. to do this we are going to use summary().



florida <- read.csv("/Users/Shep/git/SQLShepBlog/FloridaData/FL-Median-Population.csv")

# Checkout everything summary tells us  
summary(florida)

# Now isolate the column we are interested in
summary(florida$population)

# Now a little R indexing,
# the values we are interested in are the 2nd and 5th position
# of the output so we just reference those
summary(florida$population)[2]
summary(florida$population)[5]

# load the values into a variable
q1 <- summary(florida$population)[2]
q3 <- summary(florida$population)[5]

#Now that we have the variables run subset to grab the middle 50% 
x<-subset(florida,population >=q1 & population <= q3)

#And lets run the scatterplot again 
xyplot((population) ~ (MedianIncome), 
       data=x, 
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Population",
       type = c("p", "smooth"), col.line = "red", lwd = 2,
       pch=19)

Notice what happened? By removing everything outside of the IQR our observations (Rows) went from 67 counties to 33 counties, that is quite literally half the data that got identified as an outlier because of the IQR outlier methodology. On the bright side our scatter plot looks a little more readable and realistic and the regression looks similar but bit more wiggly than before.

So what to do? When you wipe out half your data as an outlier this is when you need to consult the powers that be. In real life you will be solving a problem and there will be some guidance and boundaries provided. Since this is just visualization, the stakes are pretty low. If you are in exploration and discovery phase, guess what, you just discovered something. If you are looking at this getting ready to make a predictive model, is throwing out 50% of the data as outlier data the right decision? Its time to make a decision. The decision i am going to make is to try out a different outlier formula. How about we chop 5% of both ends and see what happens? If the dataset were every single count in the US, this may be different.

To do this we are going to need use quantile().


# Using quantile will give us some control of the proportions 
# Run quantile first to see the results. 

quantile(florida$population,probs = seq(0, 1, 0.05))

#Load q05 with the results of quantile at the 5% percentile
#Load q95 with the results of quantile at the 95% percentile

q05 <- quantile(florida$population,probs = seq(0, 1, 0.05))[2]
q95 <- quantile(florida$population,probs = seq(0, 1, 0.05))[20]

#Create the dataframe with the subset 
x<-subset(florida,population >=q05 & population <= q95)

#try the xyplot again 
xyplot((population) ~ (MedianIncome), 
       data=x, 
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Population",
       type = c("p", "smooth"), col.line = "red", lwd = 2,
       pch=19)

Did we make it better? We made it different. We also only dropped 8 counties from the dataset, so it was less impactful to the dataset. You can see that some of these are not going to be as perfect or as easy as mtcars, and that's the point. Using the entire population of the US with the interquartile range may be a reasonable method for detecting outliers, but its never just that easy. More often than not my real world data is never in a perfect mound with all the data within 2 standard deviations of the mean, also called the normal distribution. If this had been county election data, 5 of those 8 counties voted for Clinton in the last presidential election, if you consider that we tossed out 5 of the 9 counties she won what is the impact of dropping the outliers? Keep in mind that 67 observations(rows) is a very small dataset too. The point is, always ask questions!

Take these techniques and go exploring with your own data sets.

Shep

Visualization, Scatterplot

Published January 6, 2017 / by shep2010

In the ongoing visualization show and tell scatterplots have come up next on my list. As I write this blog I try very hard to check and double check my knowledge and methods, I usually have a dataset or two in mind long before I get to the point I want to write about it. This time, I wanted to use the mtcars dataset to play around with the dataset and run a line through the scatter plot to show a trend, lo and behold its already been done to the exact spec I was thinking of doing. Truth be told i am not the first to do any of this, google is your friend when learning R.

So with that, I will do one set with mtcars and send you to Quick-R Scatterplots for the rest. Be careful of some of the visualizations, while nothing will stop you from creating a 3d spinning scatter plot, it is considered chart junk and there is a special website for people who create those are honored. I bet you didn’t know there was a “wtf” domain did you?

I did run into an interesting issue though that I will discuss today, it is a leap ahead, but it is important.

But, lets get some scatterplot going on first.

Below we have loaded the mtcars dataset, and run an attach(). Attach() gives the ability to access the variables/columns of the dataset without having to reference the dataset name. So, instead of mtcars$cyl we can just reference cyl in functions after the attach. It has down sides, so be careful, sort of like a global anything in programming.


data(mtcars)
mtcars
attach(mtcars)

plot(mpg,wt)

With the scatterplot we have two dimensions of data, on the left is the y axis, the weight of the vehicle in thousands of pounds, and on the bottom is the x axis, mpg or miles per gallon.

That was cool, no? Lets add “pch=19” to the next plot to make the dots a bit more visible, and add a line through the data. Abline() draws a straight line through the plot using intercept and slope, we can get the intercept and slope by passing the wt and mpg into a linear model function called lm(). Run lm(wt ~ mpg) by itself and see what you get. Make sure mpg and wt are in the order specified below, “mpg, wt” for the plot and wt~mpg for the lm function. if you dig into the lm() function you will see that we are passing in just a formula of “wt ~ mpg”, from the R documentation for lm() y must be first which is the response variable. Much, Much more on this later, just know for now, y must be first when using lm(), not x.


data(mtcars)
mtcars
attach(mtcars)

plot(mpg,wt,pch=19)
abline(lm(wt ~ mpg))

So, using our scatterplot and the lm function it would appear that as weight increases mpg decreases.

Well thats all pretty cool, but a straight line through my data gives me an idea of the trend but can be misleading if the data is wiggly in the scatter plot, or appears not to be trending. 



plot(hp, mpg, main="Scatterplot Example", 
     xlab="Horsepower", ylab="MPG", pch=19)
lines(lowess(hp,mpg), col="blue")

Using the lines() and “lowess” option you can see that the line is a little more in tune with the trend of the data. LOWESS is locally weighted scatterplot smoothing. This is much more than just intercept and slope. Depending on the package you are using, there is more than one way to get a line to fit the data.

Lets have a little fun. Hopefully you have played with the mtcars dataset a little bit and maybe even tried out some of the other base R datasets, or loaded your own. The best way to engage in topics like this is to use a dataset you have some passion or curiosity about.

I have a dataset for you on my github site, FL-Median-Population.

This dataset contains the following;

region – County name
CountyFipsCode – The Federal Information Processing Standard code the uniquely identifies the county.
population – American Community Survey estimated population
CollegeDegree – percentage of residents that have completed at least an undergraduate degree.
College – this is the sum of CollegeDegree percentage and the completed some college percentage.

We will be using the xyplot from the lattice package, and the dataset listed above, be sure to change the file location two where every you put it, or use setwd to set your working directory. For this we will start with just the population and median income. 


install.packages("lattice")
library(lattice)
  
florida <- read.csv("/Blog/FloridaData/FL-Median-Population.csv")

xyplot(population ~ MedianIncome, 
       data=florida, 
       pch=19,
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Populaton")

Hopefully your plot looks a little bit, or exactly like this one. I think this is a good example because it is an imperfect sample. Hopefully on a good day you will get something more like this, and not complete randomness. One point to notice right away is there is one dot way out of range of the rest of the dots at the top of population. Not hard to figure out that is probably the county that Miami resides in, Miami-Dade, and then four other counties coming in at over a population of 1 million. You will also notice there is one county way off to the right in median income, that is St Johns county, which is where the city of Jacksonville is located. Now the median income of Jacksonville is lower than the median income of the county, so what could be going on there?

Hmmm, this just raises more questions, it just so happens, with a population of about 27,000 Ponte Vedra Beach has a median income of $116,000 according to wikipedia, so this one city is dragging the average for the entire county of 220,257 up pretty significantly compared to other counties. So, the with the population of Miami-Dade and the median income of St. Johns being far away from the rest of the data, these are what we call outliers. For now we are going to leave them in, in the next couple of blogs i will demonstrate a method for dealing with outliers. Clearly one like the county of St. Johns will need to be handled eventually.

So from looking at the scatter plot, we can kind of make out a general direction of the relationship of income to population, but it is sort of vague. In cases like this there are a few things to do.

1. When your data looks like it has gone to crazy town, try applying a transformation function for a better graphical representation. This will change the x/y scale, but will still represent the trend of the data. More on log transforms here.



xyplot(log(population) ~ log(MedianIncome), 
       data=florida, 
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Population",
       pch=19)

2. Draw a linear regression line through it so see if there is a trend. We will get into lm() later, but it takes the (y ~ x) as model input and returns an intercept and slope, remember algebra? 🙂

There is more than one way to do this, xyplot uses the panel function, the much lengthier syntax. 



xyplot(log(population) ~ log(MedianIncome), 
       data=florida, 
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Population",
       panel = function(x, y, ...) {
       panel.xyplot(x, y, ...)
       panel.abline(lm(y~x), col='red',lwd=2)},
       pch=19)
##
## OR
##

plot(log(florida$MedianIncome),log(florida$population),pch=19)
abline(lm(log(florida$population) ~ log(florida$MedianIncome)))

3. In the previous sample we just used a lm, straight line, slope and intercept to run a line through the data, that alone does show a trend. Even if you remove the log function you still seen upward trend of greater population seems to indicate greater income.

So lets try the LOWESS again, this time with xyplot. The type parameter below is using a "p" parameter, this is the LOWESS (locally weighted scatterplot smoothing), it will take our bumpy data and smooth the line to the data. You can read up on it, we will be hitting it thoroughly later on. 



xyplot(log(population) ~ log(MedianIncome), 
       data=florida, 
       main="Population vs Income",
       xlab="Median Income",
       ylab = "Population",
       type = c("p", "smooth"), col.line = "red", lwd = 2,
       pch=19)

One thing appear to be somewhat clear from this, as the population of the county increases, the income does increase to a point hen it seems to stabilize. We will revisit this once we learn how to deal with outliers and see if it changes the trend.

There are a couple more columns in the Florida data provided that you can try on your own, see if you can visually show a relationship between college and income, or even college and population. Do more rural counties have more or less college educated population?

Damn Lies and Statistics

Published January 5, 2017 / by shep2010

Here are a few recent podcasts that are worth listening to. They all have a foundation in statistics, and if you are not questioning everything stats you here in the media, you should and you will.

Knowing statistics and statistical learning breaks down a lot of barriers in day to day life. Correlation does not mean causation is the term that rings through my head every day. Just because to variables are moving together does not mean they effect each other.

On the other hand, after listening to the four podcasts below, it not just a correlation problem, its results that cannot be reproduced problem. Its drug companies performing trials on the healthiest possible pool of subjects, imagine testing an asthma medication on an olympic athlete that has asthma, do you think that would be representative of you and me?

Hidden Brain – Encore of Episode 32: The Scientific Process

Freakonomics- Bad Medicine, Part 1: The Story of 98.6

Freakonomics- Bad Medicine, Part 2: (Drug) Trials and Tribulations

Freakonomics- Bad Medicine, Part 3: Death by Diagnosis

Shep

Stats Stuff 2, Central Tendency

Published January 4, 2017 / by shep2010

We have determined that quantitative data is essentially numeric data, or “measuring data”. Quantitative data asks how much. Knowing that, we can start to look at statistical techniques to analyze this data. To do this we will need to get some definitions out of the way, and some demonstrations to help figure out what these things are. None of them are derived from magic, though sometimes they certainly appear that way.

There is a thing called central tendency, or the measure of central tendency. It is not very hard to derive the definition from the words, it is the tendency of the things to be centered, or the center or location of the distribution of data. For the most part, as the dataset we are using increases in size, it tends to have much of the data centered in a specific location. We measure this by using mean, median, and mode.

Central tendency will be one of the very important foundations of prediction, it’s a principle that assumes all of the data will be within a certain distribution vs data all over the place. If you were to use a histogram with many bins, the data would be mound shaped. That mound means that we can probably predict other new data based on certain factors, those factors will come later.

Mean – the mean is the average, sum the data and divide by the number of values. 

(1+2+3+4+5+6+6+7) / 8 

mean(c(1,2,3,4,5,6,6,7))

Median – Basically the middle number in the data set, using (1,2,3,4,5,6,6,7) we have eight numbers in the dataset, an even number, so we take the two middle numbers add them and divide by two, in this case the Median is 4.5. In R you can run median(c(1,2,3,4,5,6,6,7)). If we had an odd number of values in the dataset as in (1,1,1,2,9,9,9), “2” is the median. It is just the middle number.


median(c(1,2,3,4,5,6,6,7))
median(c(1,2,3,4,5,6,7))
median(c(1,1,1,2,9,9,9))

Mode – Mode is the number that shows up most often in the dataset. Mode is a little tricky, there is no built in function for Mode in base R. Stack overflow has a nice mode reference here, which demonstrates the following 



Mode <- function(x) {
  ux <- unique(x)
  ux[which.max(tabulate(match(x, ux)))]
}

Mode(c(1,1,1,2,9,9))

If you are use to T-SQL that last thing may have tripped you up a bit, a function being stored in a variable. Its called a “Call by Reference”. We will get more into this at a later date as this gets into some of the power of R.

Its really not very hard, and we will be using central tendency a lot. try it out with some of the datasets. Try this out on a few datasets that ship with base R, or your favorite dataset, graph it using hist() see if you can spot some of the tendencies and do they match what you would expect using just mean, median, and mode. 



?cars
data(cars)
View(cars)

mean(cars$dist)
median(cars$dist)
Mode(cars$dist) #using the above Mode function

data(mtcars)
View(mtcars)

mean(mtcars$mpg)
median(mtcars$mpg)
Mode(mtcars$mpg)

# Use zoom in the plot pane to review the histogram, 
# check out the distributions
library(mosaic)
data(ChickWeight)
View(ChickWeight)

histogram(~weight | as.factor(Time), data=ChickWeight,type="percent")

Somewhere between this topic and the next topic there lives a thing called percentiles and quartiles.

Percentile - In statitistics a percentile is the measure indicating the value below which observations in a group fall. Yeah right, lets use an example. When occupy Wallstreet was all the rage they frequently help signs of 99%, that meant that you and i are the 99 percentile of income. Hence they were attempting to annoy anyone in the US who fell into the 1 percentile. According to this article from investopedia, you would need to make more than $456,626 AGI to be in the one percent. From that we can determine that anyone who makes less than $456,626 AGI is in the 99 percentile. To be in the 95 percentile you need to make less than $214,462 AGI per year. So, percentile is a measure of location. Where am i? Where are you?

Quartiles - In descriptive statistics, the quartiles of a ranked set of data values are the three points that divide the data set into four equal groups, each group comprising a quarter of the data. Clear as mud, well four equal groups makes sense. They are, 25%, 50%, 75%, these divide the data into four groups.

Lets look at some data. R has a base function summary(), summary is your friend. Mtcars is should be loaded already, if it is not you are a wizard at getting in memory by now. 



summary(mtcars$mpg)

#   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#  10.40   15.42   19.20   20.09   22.80   33.90

Min is the minimum value of the dataset,
1st quartile or 25 percentile is 15.42
2nd quartile or 50 percentile or median is 19.20
3rd quartile or 75 percentile is 22.80
Mean or average is 20.09
Maximum value for the dataset is 33.90

Lets use a few more words to describe whats going on above. IF the mpg of your car is 12, like my Jeep, you are in the 25th percentile. If you get 22mpg, you are in the 75th percentile and above the median (19.20) and above the mean(20.09). Why this matters will come up later, but be cognizant of where a datum falls.

You can run summary against an entire dataset as well vs just a column/variable summary(mtcars) for instance. This will provide statistics for all columns/variables in the dataset.

From the Mosaic package there is a function favstats() that is similar to summary you should check out. 


 favstats(mtcars$mpg)
  
 # min     Q1 median   Q3  max     mean       sd  n missing
 #10.4 15.425   19.2 22.8 33.9 20.09062 6.026948 32       0

Notice that sd for standard deviation, n the number of values in the dataset and missing is also listed.

More on all of this from a different writer